Trajectory Optimization with Optimization-Based Dynamics
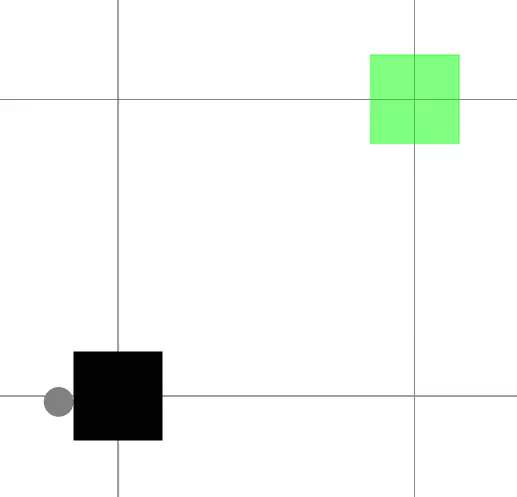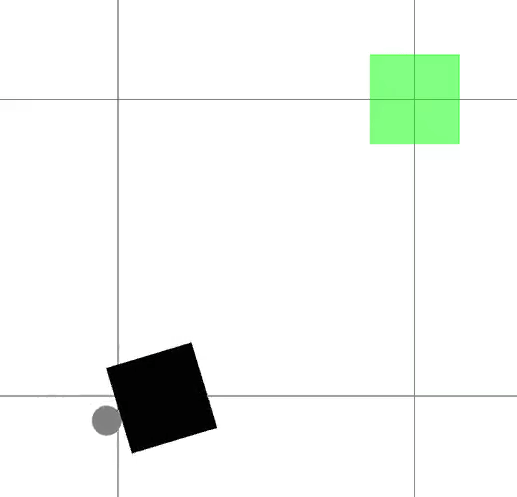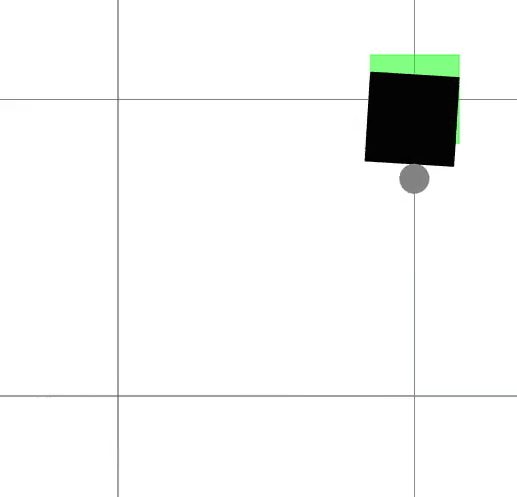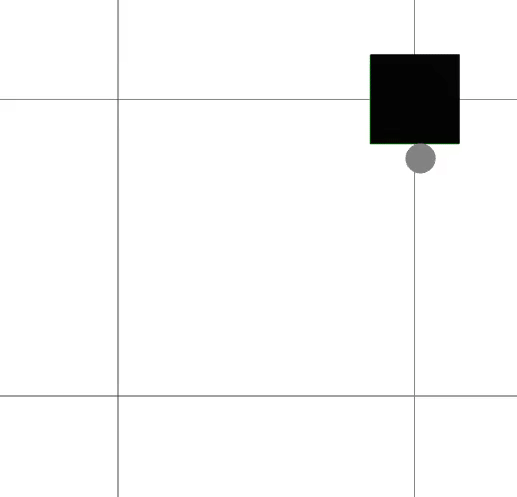
We present a framework for bi-level trajectory optimization in which a system’s dynamics are encoded as the solution to a constrained optimization problem and smooth gradients of this lower-level problem are passed to an upper-level trajectory optimizer. This optimization-based dynamics representation enables constraint handling, additional variables, and non-smooth behavior to be abstracted away from the upper-level optimizer, and allows classical unconstrained optimizers to synthesize trajectories for more complex systems. We provide a path-following method for efficient evaluation of constrained dynamics and utilize the implicit-function theorem to compute smooth gradients of this representation. We demonstrate the framework by modeling systems from locomotion, aerospace, and manipulation domains including: acrobot with joint limits, cart-pole subject to Coulomb friction, Raibert hopper, rocket landing with thrust limits, and planar-push task with optimization-based dynamics and then optimize trajectories using iterative LQR.
Code is available here.
Related Papers
|
2021 September |
Robotics and Automation Letters |



